02 Angles in a polygon

A polygon is a closed figure formed with straight sides. A triangle has 3 sides, a quadrilateral has 4, and a pentagon has 5. The angles of a triangle add up to 180 degrees. Triangles can be classified based on angles (acute, obtuse, right) and sides (scalene, isosceles, equilateral).

Triangles #

A closed figure formed with only straight sides is known as a polygon. How many sides are required to form a closed figure?

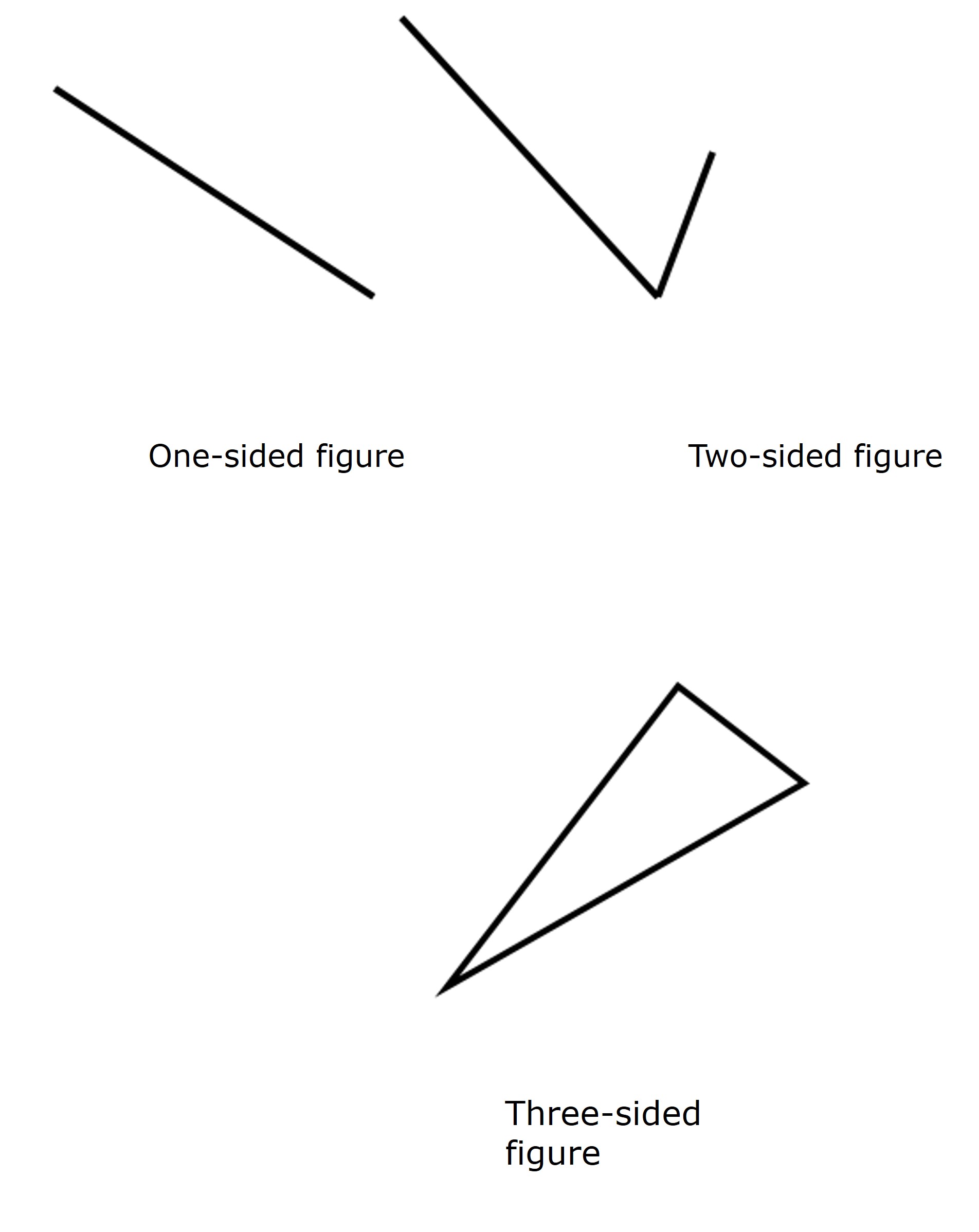
It seems that we need at least 3 sides to form a polygon, which gives us a triangle. If a polygon has 4 sides, then it is known as quadrilateral. If the number of sides in the polygon is 5 sides, then it is known as a pentagon, and so on. Additionally, if the polygon has all of its sides equal to each other, then it is known as a regular polygon. A regular polygon has all of its angles equal to each other as well, as a result of all sides being equal. A regular triangle is known as an equilateral triangle. A regular quadrilateral is known as a square.

The three angles of a triangle (any triangle) when added are equal to 180° degrees. Let’s observe the triangle ABC so we can see if this is true or not. Three angles 47.5°, 27.5°, and 105° degrees.

If we draw a line at A that is parallel to the side CB, we get two angles as shown. We see that the two angles are equal to the two remaining angles at B and C because they are alternate angles to angles at B and C, respectively. Since the line we drew was straight line, the three angles together are supplementary angles, meaning they give us a sum of 180 degrees.

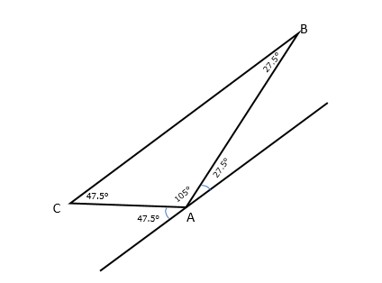
Thus, the three angles of the triangle give a sum of 180° degrees as seen in the figure.

Classification of triangles #

Based on angles #

Based on the range of angles present in the triangle, we can classify them into different types:

1. If all the angles in a triangle are less than 90° degrees, then the triangle is known as an acute-angled triangle (since angles below 90 degrees are called acute angles).

2. If one of the angles in a triangle is more than 90 degrees, we call it an obtuse angled triangle. Note that a triangle cannot have more than one obtuse angle since the sum of the three angles need to be 180 and having more than 1 obtuse angle will lead to a sum of more than 180 degrees.

3. If one of the angles in a triangle is 90° degrees, then the triangle is known as a right-angled triangle. Here are two examples of right-angled triangles.

Is more than one right angle possible in a triangle?

Theoretically, it is. If two of the three angles are 90° then the sum of those becomes 180°. However, there are three angles in a triangle. If two of the angles in the triangles give a sum of 180° degrees already and the sum of three can’t exceed that number, the third must be zero. What do you think a triangle with 90°, 90°, and 0-degree angles will look like? We can’t construct such a triangle, obviously!

Based on sides #

Triangles can also be divided into different types according to the equality of sides.

1. If none of the sides are equal to each other in a triangle, then it is known as a scalene triangle.

2. If two of the sides are equal, then such triangles are known as isosceles triangles. The two angles opposite to the equal sides are known as base angles of an isosceles triangle and they are equal as well.

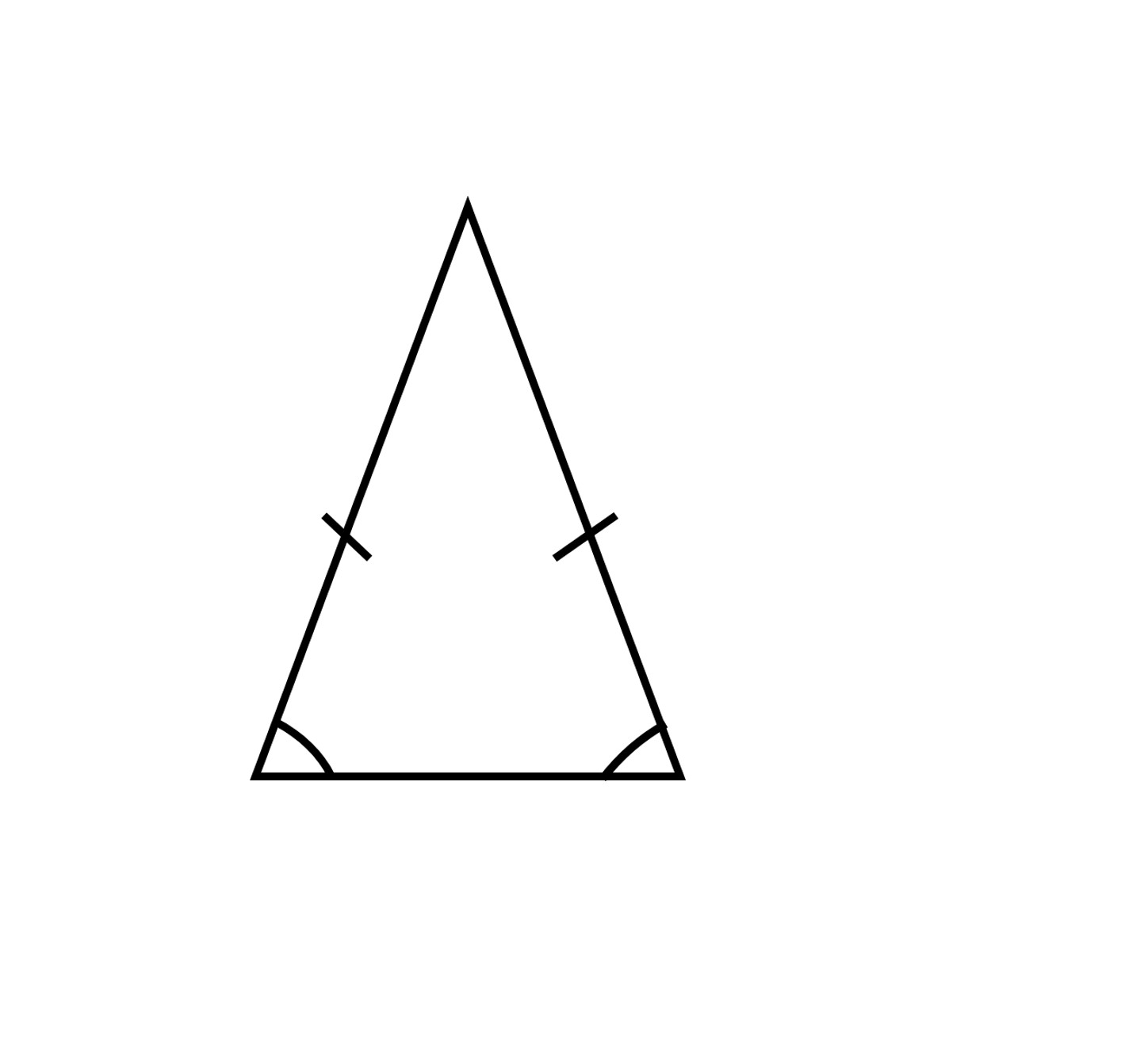
3. If all three sides are equal, then such a triangle is known as an equilateral triangle. Since the sides are equal, each angle opposite to them will also be equal in magnitude.

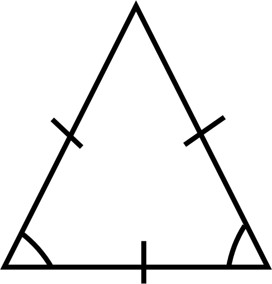
We know that the sum of the three angles in all kinds of triangles is 180°. If one of the angles is supposed to be ‘p’, all of the angles will be ‘p’ in an equi;ateral triangle.

p + p + p = 180°
or, 3p =180°
or, p = 180°/3 = 60° degrees

Therefore, in all equilateral triangles, the internal angles are 60° degrees each.

Exterior angle of a triangle #

Suppose we have a triangle BAD as shown in the figure.

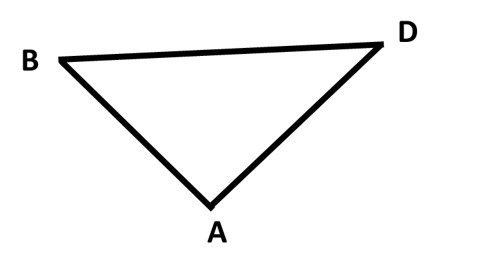
Then according to what we have studied recently, the angles formed at the three vertices; A, B, and D are summed to get 180° degrees. Now, let’s extend line BD to C.

There are two angles formed at point D, one is ∠ADC and the other is ∠ADB. The sum of the two is also 180° degrees because they formed a straight line, making them supplementary angles. We have two equations as follows: ∠ADC + ∠ADB = 180
(∠ABD + ∠BAD) + ∠ADB = 180°

When we compare the two equations, we get,
∠ADC = ∠ABD + ∠BAD (They need to be equal since ∠ADB and 180° are equal in both equations)

This can be translated into a theorem that says that the exterior angle (∠ADC) of a triangle is equal to the sum of two opposite interior angles (∠ABD + ∠BAD). This is true for lines extended from any side. Just keep in mind that they need to be an extension on one of the sides (Like DC is extended from BC).

Quadrilaterals #

After learning about the triangle, we move on to the polygon made with four sides. A polygon with 4 sides is a quadrilateral. Based on different relations and specialties among the dimensions of the quadrilateral, it is classified into different types. Parallelogram, rhombus, rectangle, kite, trapezium, and square are all types of quadrilaterals. They are called quadrilaterals because they possess 4 sides.

Quadrilaterals with opposite sides that are parallel are parallelograms. In such cases the opposite sides are equal as well. The figure above is a parallelogram.

In a parallelogram, if all of the four sides are equal with each other, it is called a rhombus. The figure given above is that of a rhombus.

If a parallelogram has all of its angles 90 degrees or right angles, then such a shape is known as a rectangle. Just like in parallelogram, the opposite sides are equal as well as parallel to each other. The figure below is that of a rectangle.

If in a rectangle, all the sides are equal to each other then the shape is a square. A square is given below.

Squares are the most symmetrical quadrilateral with all of the sides and angles equal. They possess all the properties possessed by parallelograms, rhombi (plural of rhombus), and rectangles. If you don’t believe it, you can go back and tick all the properties it possesses.

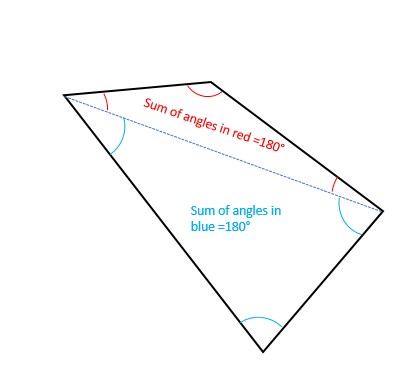
The total sum of angles in a triangle is 180. What about a quadrilateral? We can divide a quadrilateral into two triangles when any two of the opposite corners are joined with a diagonal. The sum of angles in both triangles is 180 and since we have two triangles, it means that the total sum of all the angles in the quadrilateral is 2 x 180° = 360° degrees. Simple, right?

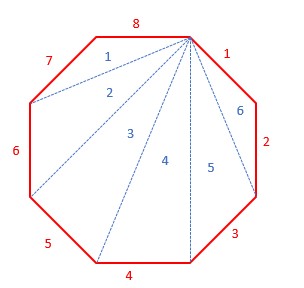
Since there needs to be two opposite corners to form a diagonal, a polygon of ‘n’ sides will have ‘n-2’ triangles possible to form inside it. You can also find this by generalization. A quadrilateral can give us 2 triangles (4 sides - 2). A pentagon can give us 3 triangles (5 sides - 2). A hexagon can give us 4 triangles (6 sides - 2). So, the sum of the internal angles is the number of triangles times 180 degrees, which is equal to (n-2) x 180°.

If we know the number of sides of a regular polygon, we can easily find the measure of the interior angle as well.

We know the total sum of n angles in the polygon. It is given by (n-2) x 180°. There are ‘n’ angles in a n-sided polygon. If the polygon is regular as well, then all of the angles are equal to each other. Therefore, each internal angle in an n-sided regular polygon is [(n-2)/n] x 180° (Basically, total sum of angles divided by number of sides).

In a regular pentagon, each internal angle measures, (5-2)/5 x 180° = ⅗ x 180° = 108°

In a regular hexagon, each internal angle measures, (6-2)/6 x 180° = ⅔ x 180° = 120°