01 Introduction to Expressions
What are expressions?
Expressions are not just numbers like 14. They have different operators like addition (+), multiplication (x), subtraction (-), and division (÷). Here’s an example:
If we multiply 3 and 4, we get 12. We can write this as 3 x 4 or 12. Both are numerical expressions. Here, we see that 3 x 4 is equal to 12 and 12 is obviously equal to 12 as well. So, numerical expressions always have a value (in this case, 12) or have some quantity they are equivalent to.
Some other examples of numerical expressions are:
2 x 3 + 5
9 - 5 x 12
12 / 6
45
10001
When we see a math problem like 100 - 3, how can we explain what it means? There are two ways to think about it! One way is to think about what we need to do to 100 to get the answer. We need to take away 3, so the answer is 97. Another way is to think about the expression itself as a value. It means a number that is 3 less than 100, which is also 97. Both ways give us the same answer!
As we talked about before, expressions are mathematical sentences that could equate to or could be equivalent to a value.(sometimes they could be equivalent to other expressions. Keep in mind that the value by itself (97) is also an expression as well) This is what we call the ‘value of an expression’.
Let’s check out another example to understand this better. In the US Senate, there are 2 senators chosen from each state. So, to find out how many senators there are in total, we need to know how many states there are. There are 50 states in the US, so how many senators are there?
Since each state has 2 senators, we can add 2 fifty times in a row. 2 + 2 + 2 + 2……. (50 times)
We can also write this repeated as multiplication to get 50 x 2, which means 50 times 2.
Both numerical expressions are equal to 100. Both mathematically and contextually, the two expressions we have formed are equivalent, hence are called equivalent expressions. Mathematically, they are both equal to 100. Contextually, they mean the same thing - the total number of senators.
We’ll learn more about this in the future!
Letters in expressions
Let’s talk about variables! They’re like letters or symbols that we use in expressions. You might be wondering why we use letters instead of numbers. Well, sometimes we don’t know what the number is, so we use a letter to represent it for the time being. It’s like a mystery number that we can find later!
When we look at 9 - 3, it means we need to take away 3 from 9. Easy, right? Well, sometimes we see expressions like 50 - a. Similar to before, this means we need to take away ‘a’ from 50. t may also be expressing a number that is less than 50 by some value ‘a’. You might be wondering, how can we subtract a letter from a number? But don’t worry, we’re not really subtracting a letter.
When we do math with numbers, we can add, subtract, multiply, and divide them. But when we don’t know the value of something, we use a letter to stand in its place. It’s like having a friend save your seat at a restaurant. The letter doesn’t get added, subtracted, multiplied, or divided by a number. The letter is special because it represents a quantity that we don’t know yet, unlike numbers that we already know.
Some examples will hopefully help you understand this better.
Let’s say you want to buy a chocolate and luckily, the store is offering a discount of 30 cents on all chocolates. If a chocolate is marked as $3, you can figure out the price by subtracting the discount: $3 - $0.30 = $2.70. If another chocolate is marked as $4.70, you can do the same calculation: $4.70 - $0.30 = $4.40. But what if there are lots of different prices for chocolates? You could do the math for each one, or you could use a special symbol to stand in for the price. Look at the table given below.
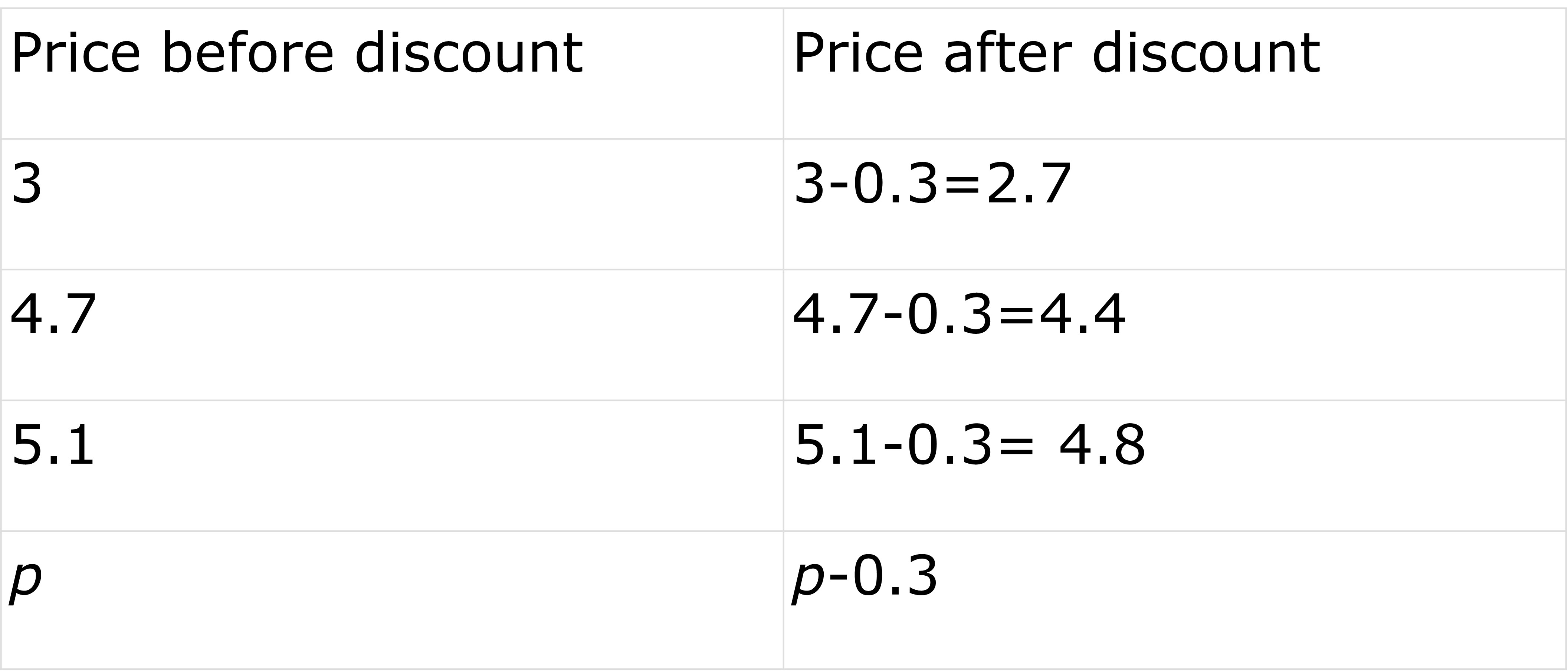 We all know that not all chocolates cost the same. And we also know that we always have to pay 30 cents less than the price that's written on the package. But what if we had a way to talk about all the different prices of toffees at once? That's where the letter "p" comes in handy! If "p" stands for the price of a chocolate before the discount, then "p - 0.3" tells us how much we need to pay for it after the discount.
Basically, we substitute the unknown or varying costs of different chocolates with a letter such as p. Due to this the discounted prices of different chocolates (shown in different rows) can be explained with the single expression of p - 0.3.
We all know that not all chocolates cost the same. And we also know that we always have to pay 30 cents less than the price that's written on the package. But what if we had a way to talk about all the different prices of toffees at once? That's where the letter "p" comes in handy! If "p" stands for the price of a chocolate before the discount, then "p - 0.3" tells us how much we need to pay for it after the discount.
Basically, we substitute the unknown or varying costs of different chocolates with a letter such as p. Due to this the discounted prices of different chocolates (shown in different rows) can be explained with the single expression of p - 0.3.The letter “p” is just a stand-in for the real price. If someone tells you a specific price, like 4 dollars, that means the original price of the toffee was 4.3 dollars. And if they say 4.8 dollars, that means it’s for a chocolate that originally cost 5.1 dollars. Easy, right?
Let’s look at another expression with a variable. Suppose there is a 10 percent discount on all types of eye checkups and treatment fees. If a treatment costs 100 dollars, after the discount, it will cost 10 dollars less. So the patient has to pay only 90 dollars. Original - 10% of original price 100 -10% of 100 =100 - (10/100) x 100 =100-10 =90
If the cost of another treatment was 75 dollars, then the patient has to pay: 75 - 10% of 75 =75-0.1 x 75 =75-7.5 =67.5 This process will be the same for all values. Like before, we can replace all values of treatments that keep changing with a placeholder, say “d”. Now, we have the value of each treatment as: =d - 10% of d =d - 10/100 x d =0.9d If we put 100 in place of d it will be 0.9 x 100 = 90 and if we put 75 in place of d it will be 0.9 x 75 = 67.5. This corresponds with the answers we found earlier. 0.9d is the expression that gives the money a patient has to pay following the discount available. Expressions like these, with a letter in them are no longer numerical expressions, but are called algebraic expressions. The letters are variables and the numbers are constants because they do not change in the given context.
Variables
The letter or symbol we use for a variable doesn’t matter and has nothing to do with the quantity we are representing. It can be any letter or symbol we want. For example, if we say an apple costs p or a, it’s just to make things easier, not because p or a stands for a specific price of an apple. It’s also important to remember that the letters don’t stand for the object itself, but for something that describes the object (like an attribute of the object). So if we use f as a variable in a problem about fish, it could mean the weight of the fish, the number of fish, or the price of the fish. It does not mean fist in itself. Say the number of fish caught in a net is 55 and each fish weighs roughly around the same. If we write the total weight of fishes as 55f (55 multiplied by f), it means we are multiplying 55 by the weight of a fish, which we are denoting as ‘f’. 55f does not mean that there are 55 fishes, since 55 itself is enough to convey that information.
Sometimes letters are used to represent units of measurement, like “m” for meters or “lb” for pounds. So keep in mind not to confuse letters used for units and letters used as variables.
It’s also important to use different letters for different quantities in the same context, even if they’re unknown. For example, if you’re guessing the ages of two cousins and you use “x” for one, you can’t use “x” for the other because it’s unlikely that they’ll be the same age.
Similarly, if you use “t” to represent the number of oranges in a scenario, you shouldn’t use “t” again to represent the weight of the oranges.
Most times when you see a letter in an expression, it’s a variable. But there are times when special symbols like π (pi) are used, which is not a variable since it always means the same thing. Pi is used a lot in math problems about circles and it always equals 3.14. Another symbol like this is e, which we’ll learn more about later on.