01 Introduction to 3D objects and volume
Jumping from 2D to 3D: Introduction
Total Surface Area
It is easy enough now to find the area of different shapes, like triangles and rectangles. But in real life, things aren’t always flat like a sheet of paper, shapes aren’t drawn on flat sheets. You might see a triangle or rectangle in real life, but they won’t be perfectly flat. There will be a little bit of thickness, even if it’s very thin.

Have you ever seen a Rubik’s cube? It’s a cube-shaped puzzle with different colors on each side as shown. It has three sides facing different directions, which means it has three dimensions.

To describe the size of a Rubik’s cube, we need to measure the length of each side in all three directions. This measurement is called the dimensions, and since the object spans over three directions, this object has three dimensions. So these types of objects are called 3D objects in short. The first property of a 3D object is its face. Faces are the surfaces of a 3D object. If we look at the cube from two directions, we can see a face. For example, if we only see the pink and green lines, we see a red face. If we only see the white and green lines, we see a blue face. Thus, there are six ways to look at a cube: front, back, top, bottom, left, and right. Each way shows a different face. We can only see three faces in the picture, but there are three more on the other side that we can see by rotating the cube.
The straight lines where the square faces meet are called edges. A cube has 12 edges, but we can only see 9 in the picture.
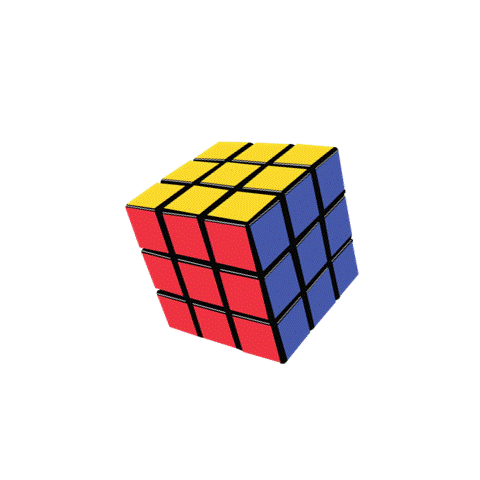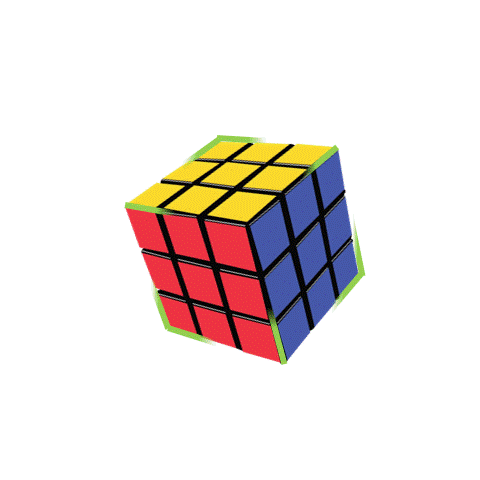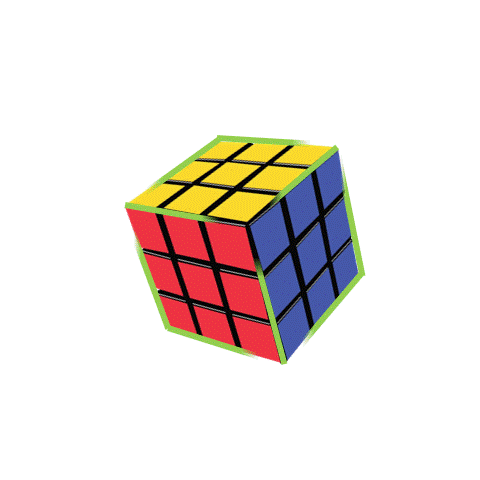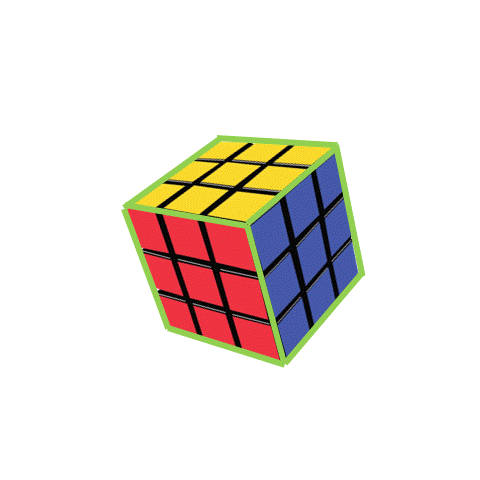
The corners of the cube are where the edges meet and there are 8 corners in total, but we can only see 7 below.
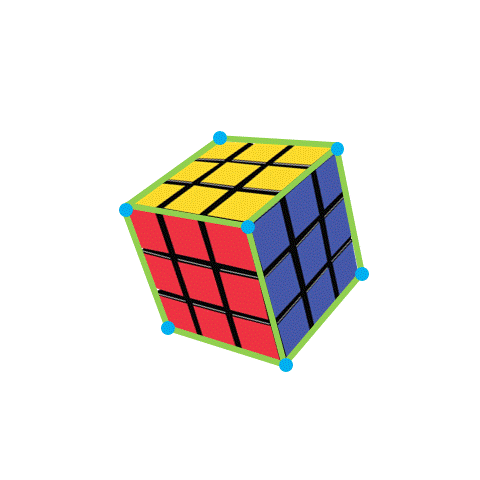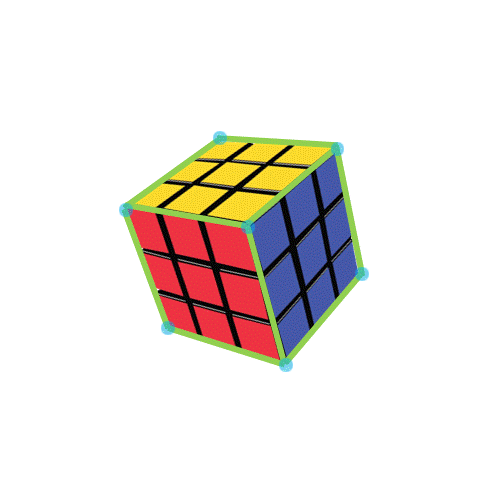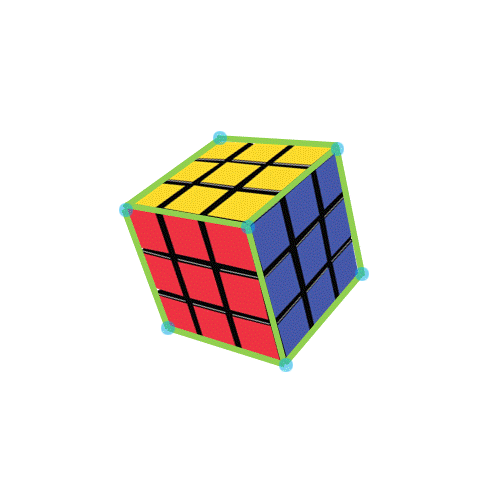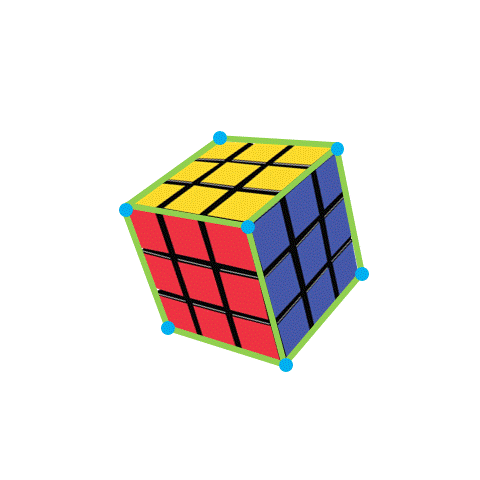
The number of edges and corners in an object depends on how many faces it has. If the sides of a cube aren’t equal, then it’s called a cuboid. We’ll learn how to find the total surface area of a cuboid later.
We’ll first start with the cube.
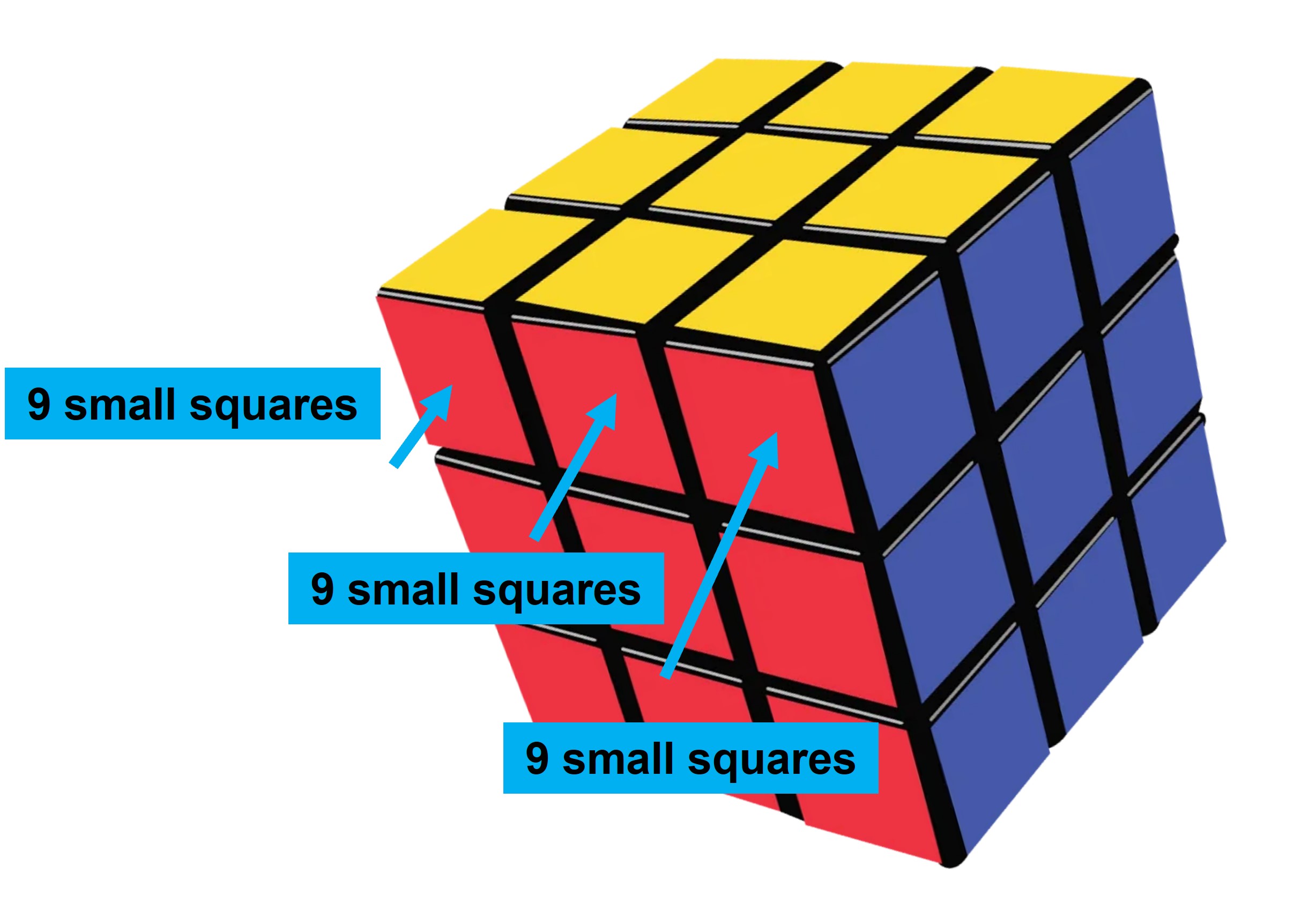
We can see that each face of a Rubik’s cube also has smaller squares on it, and they’re all the same size. We can count the number of squares on each face to measure its surface area. For example, the red face that we see from the front has nine squares. Likewise, each of the others faces has nine squares since they are all of the same size.

If each small square has a unit surface area, then the red face has an area of 9 square units. Like the red face, it is the same with the blue, yellow and other remaining faces. The cube has six sides, each with an area of 9 square units. When we add up all the areas of the sides, we get the total surface area of the cube to get a total of 54 square units (9+9+9+9+9+9).
Total surface area is the sum of all visible surfaces of an object. Visible faces mean all faces of the object, even the hidden ones that can’t be observed (when drawn on paper) without rotating the object. We can analyze which surfaces are part of the total surface area by questioning ourselves and thinking of It like covering the cube (or shape) with paper - and looking at which sides to cover.
When we have a 3D object with different shaped faces, we find the area of each shape and add them up to get the total surface area.
Volume
While area is the space that a 2D object takes up in two directions, volume is how much space a 3D object takes up in three different directions.
For example, let’s look at the Rubik’s cube. We can find its volume by figuring out how many smaller cubes fit inside it. This is similar to us finding the area by asking how many squares of unit length fit inside a shape.If we think of each small cube having a side of 1 unit (in all three directions), we can say that 27 such cubes fit inside the whole cube. We can find this by adding 9 + 9 + 9 for each row. Or by multiplying the length, breadth, and height of the cube, giving us 3 x 3 x 3.
So the volume of the cube is 27 square units? Not quite.The unit of volume is different from that of area or total surface area. Since we are measuring how much space is taken up by the cube in three directions, volume measures three different directions, hence the unit will be cubic units (cubic meaning 3 here). So the volume of the cube is 27 cubic units. If the smaller cube had a measure of 1 cm on all sides, the volume of the cube would be 27 cubic centimeters.
Interestingly, just like how the smaller squares used to measure the area of the bigger shape had an area of itself, the small cubes used to measure the volume of the Rubik’s cube also has its own volume. Since we do not have even smaller cubes making up the small cubes, we use the length, breadth, and height method. This gives us 1 x 1 x 1 = 1 cubic unit as the volume of each small cube.
If this is a little confusing, don’t worry. We’ll look into this more when we talk about specific 3D objects later.