02 Equivalent Ratios

What are equivalent ratios? #

With knowledge on how to write ratios and represent them using diagrams, we will now move on to understanding what can be done to these ratios, while keeping the relationship the same.

Look at the image of a flower given below:

The different ratios you can write for the image is:

a. The ratio of hexagons to trapezoids is 6:2.
b. The ratio of trapezoids to hexagons is 2 to 6.
c. There are 3 hexagons for every trapezoid. And so on…..

Now, say you have two such flowers:

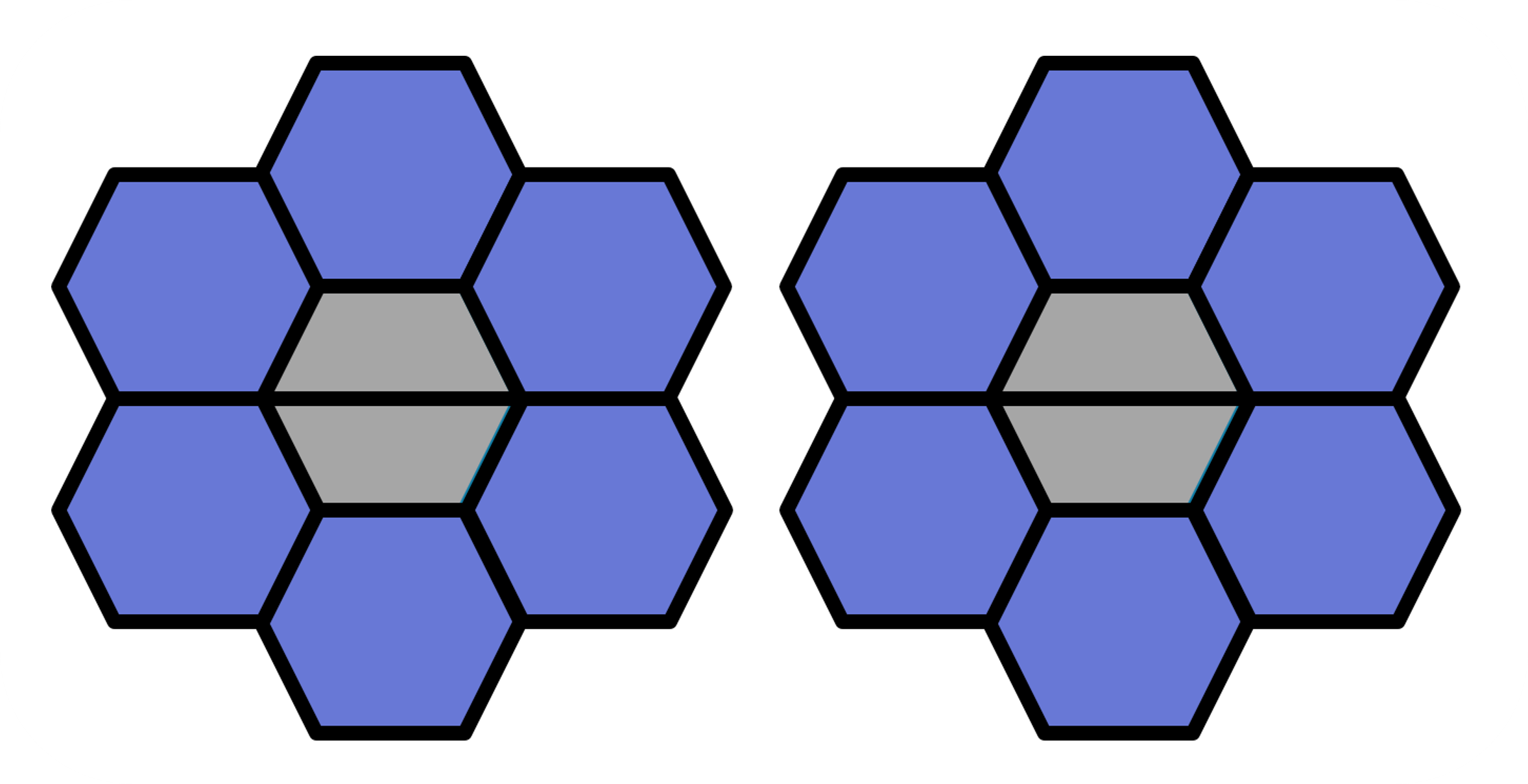
What would be the ratio of hexagons to trapezoids? It would be 12 to 4. Finding this is easy enough, we simply count the number of hexagons and trapezoids. But, we can also see that each number in one copy of the picture can be multiplied by 2 to find the number of each shape in two copies. Both numbers in 6:2 can be multiplied by 2 to get 12:4, which is actually what happened since we have two copies of the same image of the flower.

This is kind of the same as when we divide both numbers by the biggest factor to get the simplest form. Just like how the simplest form still maintained the relationship between the two quantities, multiplying the same number also maintains the same relationship. Both ratios of hexagons to trapezoids (6:2 and 12:4) will have the same simplest form of 3:1 as well. What we can conclude from this is that you can actually multiply both sides of a number of the ratio by the same number to get new ratios, which will have the SAME RELATIONSHIP. Such ratios are called equivalent ratios. We will look at an example to understand this better, also seeing how exactly the relationship remains the same.

A recipe for lemonade says, “Mix 5 spoons of lemon juice with 2 cups of water.” To double this recipe, we would use 10 spoons of lemon juice with 4 cups of water. To triple this recipe, we would use 15 spoons of lemon juice with 6 cups of water. This much should be obvious. We can also easily make ratios of spoons of lemon juice to cups of water for each -> 5:2, 10:4, and 15:6. The following diagram shows us all three ratios for different batches of lemonade.

We say that the ratios 5:2, 10:4, and 15:6 are equivalent. Even though the amounts of each ingredient within a single, double, or triple batch are not the same, they would make the taste of lemonade and we get the double and triple batches by multiplying the ingredients in the single batch by 2 and 3. (You can also check if they are equivalent or not by looking at the relationship between the two quantities (here, lemon juice and water). In each case, the spoons of lemon juice are 2.5 times the cups of water.)

P.S. Do you think you would get an exact copy of the flower if the new ratio of hexagons to trapezoids was 18 to 5? Think of this, maybe try making a diagram to confirm. We will look at this and other questions in the exercise and help you answer it properly.